[Algorithm] 그래프 탐색 알고리즘(DFS, BFS)
Algorithm/Concept 2023. 10. 12.
반응형
목 차
- DFS와 BFS
- 구현 방법
- 대표 문제 유형
DFS와 BFS
DFS: 깊이 우선 탐색, 재귀 함수를 사용하여 구현하는 것이 일반적이다. 재귀를 타고타고 탈출 조건에 도달하고, 그 다음에 파라미터를 하나씩 바꿔 가면서 정답을 찾는 방식.
BFS: 너비 우선 탐색, Queue나 LinkedList를 사용하는 것이 일반적이다.
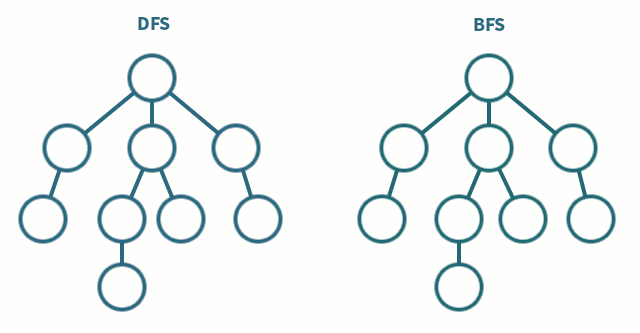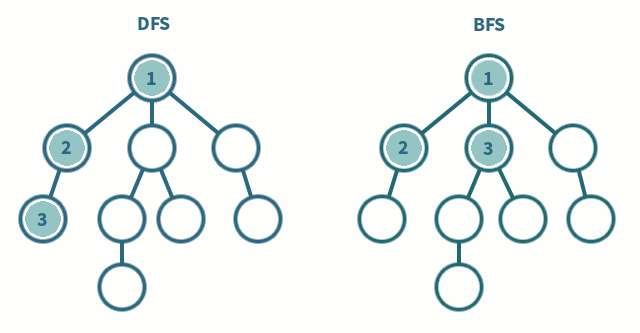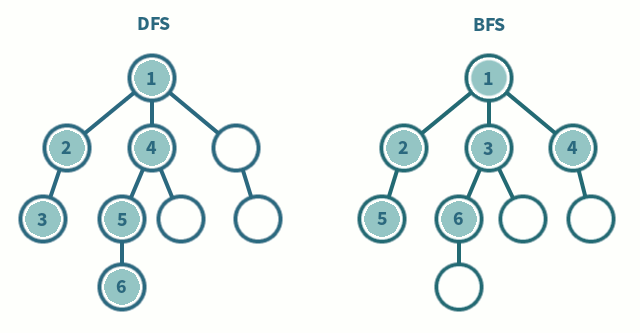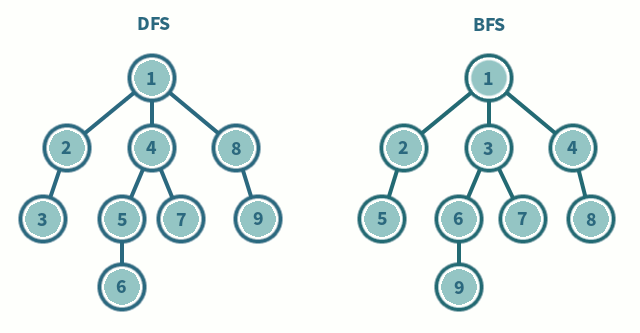
DFS와 BFS의 장단점
DFS
장점
- 현재 경로상의 노드만 기억하므로 적은 메모리를 사용한다.
- 재귀함수를 사용하여 구현이 BFS 보다 간편하며, 코드 검증이 쉽다.
단점
- 비효율적인 경로를 탐색하는 경우가 있다.
- 가장 먼저 찾은 경로가 최단 경로라는 보장이 없다.
BFS
장점
- 시작노드에서 가장 가까운 노드부터 탐색하기 때문에 최단 경로를 보장한다.
단점
- 모든 노드를 큐에 저장하므로 탐색 범위가 넓어질수록 많은 메모리를 사용하게 된다.
- 큰 데이터에서는 탐색 범위가 너무 넓어져서 비효율적일 수 있다.
구현 방법
DFS
재귀함수는 일반적으로 탈출조건을 먼저 작성한다.
function fibonacci(n) {
if (n <= 1) return n; // 탈출조건
return fibonacci(n - 1) + fibonacci(n - 2); // 재귀
}
console.log(fibonacci(5)); // 출력: 5 (피보나치 수열의 5번째 항)
BFS
Queue에 넣고 dequeue(pop)을 할 때마다 pop 된 노드에 근접한 노드를 다시 enqueue(push)를 하는 방식이다.
const N = 5;
const K = 17;
const arr = new Array(100001).fill(0);
const queue = [];
queue.push([N, 0]);
while(queue.length){
const [item, time] = queue.shift();
if(item == K){
console.log(time);
break;
}
if(item - 1 >= 0 && arr[item - 1] == 0){
queue.push([item - 1, time + 1]);
arr[item - 1] = 1;
}
if(item + 1 <= 100000 && arr[item + 1] == 0){
queue.push([item + 1, time + 1]);
arr[item + 1] = 1;
}
if(item * 2 <= 100000 && arr[item * 2] == 0){
queue.push([item * 2, time + 1]);
arr[item * 2] = 1;
}
}
대표 문제 유형
1. 경로탐색 유형(최단 거리, 시간)
2. 네트워크 유형(연결)
3. 조합 유형(모든 조합 만들기)
(출처: 유튜버: 개발자로 취직하기, 영상ID = "BsYbdUnKZ-Y")
반응형
'Algorithm > Concept' 카테고리의 다른 글
| [알고리즘] 플로이드 워셜(Floyd-Warshall) (0) | 2024.02.06 |
|---|---|
| [알고리즘] 최소 스패닝 트리(MST) (0) | 2024.01.25 |
| [알고리즘] CounterClockWise(CCW) (0) | 2023.12.14 |
| [알고리즘] 다익스트라(Dijkstra algorithm)와 우선순위 큐(MinHeap) (0) | 2023.11.14 |
| [Algorithm] 다이나믹 프로그래밍(DP) 개념 및 적용 (0) | 2023.07.29 |
![[알고리즘] 최소 스패닝 트리(MST)](http://i1.daumcdn.net/thumb/C300x300/?fname=https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fb7LZSi%2FbtsDVnDzaLQ%2FP2uhefvHXM3kCKZhVY4wVK%2Fimg.png)

![[알고리즘] CounterClockWise(CCW)](http://i1.daumcdn.net/thumb/C300x300/?fname=https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcGDBg0%2FbtsBXJB21wC%2FGUYzzVjuUWU3r8nTudX9o0%2Fimg.png)
![[알고리즘] 다익스트라(Dijkstra algorithm)와 우선순위 큐(MinHeap)](http://i1.daumcdn.net/thumb/C300x300/?fname=https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FDk5kQ%2FbtsAbbT7Uzk%2FUx13p6MSc5icYWtOCWZ9K0%2Fimg.png)
![[Algorithm] 다이나믹 프로그래밍(DP) 개념 및 적용](http://i1.daumcdn.net/thumb/C300x300/?fname=https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FXlVEs%2FbtspmWMf1XC%2F7mwpwMFLoCBN5ykrjccqI1%2Fimg.png)